Construction de classes par héritage et composition Encapsulation
NB : Les exemples illustrant ce TD proviennent de la logique séquentielle, mais ce n'est pas un TD d'architecture des ordinateurs !
Le but de ce TD est d'apprendre à construire des objets complexes à partir d'objets simples par héritage et par composition
- Portes logiques
- Circuits séquentiels
|
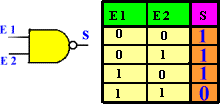
Les portes ET-NON possèdent plusieurs entrées: e1, e2, e3, e... |
|
|
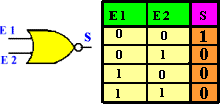
Les portes OU-NON possèdent plusieurs entrées: e1, e2, e3, e... |
|
Examiner ces portes logiques. Qu'ont-elles en commun ?
Définir une classe TPORTELOGIQUE regroupant les caractéristiques communes de ces portes, avec un constructeur et tous les mécanismes d'encapsulation.
Ecrire les classes TNAND et TNOR héritant de la classe TPORTELOGIQUE et possédant une méthode S qui définit la valeur de sortie en fonction des états E1 et E2
Ecrire un programme permettant d'instancier et de tester des objets de ces classes
Les circuits séquentiels dépendent du temps qui font intervenir les notions d'ordre et de durée. L'état de sortie dépend de se qui se passe avant: dans ce cas ce sont les opérations précédentes qui déclenchent les suivantes, c'est une question d'ordre. L'état de sortie dépend aussi du temps qui permet la combinaison des entrées et l'appartion du résultat de sortie.
2.1 Les bascules R.S
Les bascules sont des bistables qui peuvent prendre deux états. Les bascules sont asynchrones, possèdent deux entrées nommées S et R et deux sorties: nommées Q et Q . Les sorties: Q et Q sont toujours complémentaires. L'entrée S (set) met la bascule au travail et la sortie Q est au niveau 1. L'entrée R (reset) remet la bascule au repos et la sortie Q au niveau zéro.
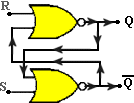
Les bascules RS sont réalisées avec des circuits NOR. Les entrées sont actives à l'etat bas (niveau zéro). Elles agissent lorsque les entrées (soit S, soit R) prennent le niveau zéro. Si S = R = O il y a état indéterminé.
On envoie séparément et alternativement les signaux sur S et R. Si deux niveaux identiques sont appliqués en même temps sur les 2 entrées il y a indétermination.
|
|
TABLE DE VERITE | |||
|
Etat initial Qn |
S |
R |
Etat final Qn+1 | |
|
1 |
1 |
0 |
1 | |
|
1 |
0 |
1 |
0 | |
|
1 |
1 |
1 |
? | |
|
0 |
1 |
0 |
1 | |
|
0 |
0 |
1 |
0 | |
|
0 |
0 |
0 |
0 | |
|
0 |
1 |
1 |
? | |
On cherche à écrire une classe modélisant une bascule TRS. Est-ce judicieux de la faire hériter de la classe TPORTELOGIQUE ou d'un de ses descendants ?
Ecrire une classe modélisant une bascule TRS composée de 2 circuits NOR avec tous les mécanismes d'encapsulation à savoir
- Le constructeur et le desctructeur
- Les méthodes GetS, GetR, GetQ, GetQB pour obtenir l'état des variables correspondantes
- Les méthodes SetS, SetR pour changer l'entrée de la bascule et calculer un nouvel état
- une méthode pour afficher l'état de la bascule (R,S,Q,QB)
Ecrire un programme permettant d'instancier et de tester un objet de cette classe
2.2 Bascule R.S.T ou R.S.Clock
La bascule R.S.T. est une bascule pour laquelle les entrées S et R ne sont prises en compte qu'en coïncidence avec un signal de commande. Ce signal peut être fourni par une horloge, nous avons alors une bascule synchrone. Ce circuit peut être réalisé de la façon suivante.
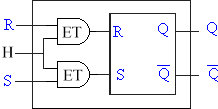a pour représentation symbolique
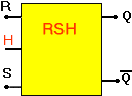
Lorsque le signal de commande, noté ici H, est à 1 la bascule fonctionne comme indiqué précédemment et les sorties suivent les variations des entrées S et R. Par contre, lorsque le signal de commande est à 0, la bascule est bloquée : Q est indépendant des éventuels changements de S et R. L'état mémorisé correspond au dernier état avant le passage de la ligne de commande H de 1 à 0.
Ecrire une classe TRST héritant de la classe RST, permettant de modéliser une bascule RST
On réécrira notamment :
- Le constructeur
- Les méthodes SetS, SetR pour changer l'entrée de la bascule en fonction de H
- La méthode permettant d'afficher l'état de la bascule
On ajoutera :
- Les méthodes SetH, GetH pour encapsuler l'horloge
Ecrire un programme permettant d'instancier et de tester des objets de ces classes
2.3 Bascules J-K
La bascule J-K permet de lever l'ambiguïté que nous avons observé lorsque R = S = 1. Ceci peut être obtenu en asservissant les entrées R et S aux sorties selon le schéma logique suivant :
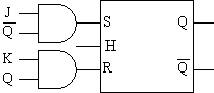
est représenté par
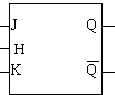
Ce qui nous permet de construire la table de vérité de la bascule J-K :
|
Jn |
Kn |
Qn |
|
S |
R |
Qn+1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
Nous constatons que nous ne rencontrons jamais la combinaison R = S = 1. Cette table peut se résumer sous la forme suivante :
|
Jn |
Kn |
Qn+1 |
|
0 |
0 |
Qn |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
Qn |
Ecrire une classe TJK, modélisant une bascule JK, héritant de la classe TRST
NB : Il suffit d'écrire 2 méthodes SetJ et SetK
Ecrire un programme permettant d'instancier et de tester des objets de ces classes
Corrigé
{*************************** CLASSE TPORTELOGIQUE ************************}
Type TPorteLogique = class
Protected
e1,e2 : boolean;
Public
Constructor Create(e1,e2:boolean);
Procedure SetE1(v:boolean);
Procedure SetE2(v:boolean);
Function GetE1 : boolean;
Function GetE2 : boolean;
end;
Constructor TPorteLogique.Create(e1,e2:boolean);
Begin
Self.e1 := e1;
Self.e2 := e2;
End;
Procedure TPorteLogique.SetE1(v:boolean);
Begin
e1 := v;
End;
Procedure TPorteLogique.SetE2(v:boolean);
Begin
e2 := v;
End;
Function TPorteLogique.GetE1:boolean;
Begin
GetE1 := e1;
End;
Function TPorteLogique.GetE2:boolean;
Begin
GetE2 := e2;
End;
{********* CLASSES TNAND et TNOR(héritent de TPORTELOGIQUE) **************}
Type TNAND = class(TporteLogique)
Public function S : boolean;
end;
Type TNOR = class(TporteLogique)
Public function S : boolean;
end;
function TNAND.S : boolean;
begin
S:= not (e1 and e2)
end;
function TNOR.S : boolean;
begin
S:= not (e1 or e2)
end;
{********************* Bascule RS : CLASSES RS ******************}
Type TRS = class
protected
Nor1, Nor2 : TNOR; {Composée de 2 TNOR}
public
procedure SetS(valeur:boolean);
procedure SetR(valeur:boolean);
Function GetS : boolean;
Function GetR : boolean;
Function GetQ : boolean;
Function GetQB : boolean;
procedure afficher;
constructor Create;
destructor Destroy;
end;
constructor TRS.Create;
begin
Nor1 := TNOR.Create(false,true);
Nor2 := TNOR.Create(false,false);
end;
destructor TRS.Destroy;
begin
Nor1.Destroy;
Nor2.Destroy;
end;
Function TRS.GetS : boolean;
begin
GetS := Nor2.GetE2;
end;
Function TRS.GetR : boolean;
begin
GetR := Nor1.GetE1;
end;
Function TRS.GetQ : boolean;
begin
GetQ := Nor1.S;
end;
Function TRS.GetQB : boolean;
begin
GetQB := Nor2.S;
end;
procedure TRS.SetS (valeur : boolean);
begin
Nor2.SetE2(valeur);
Nor2.SetE1(GetQ);
Nor1.SetE2(GetQB);
end;
procedure TRS.SetR (valeur : boolean);
begin
Nor1.SetE1(valeur);
Nor1.SetE2(GetQB);
Nor2.SetE1(GetQ);
end;
procedure TRS.afficher;
begin
writeln('R:',GetR,' S:',GetS,' Q:',GetQ,' QB:',GetQB);
end;
{*********** Bascule RST : CLASSES TRST hérite de TRS ******************}
Type TRST = class(TRS)
protected
h : boolean;
public
procedure SetS(valeur:boolean);
procedure SetR(valeur:boolean);
procedure SetH(valeur:boolean);
function GetH : boolean;
procedure afficher;
constructor Create;
end;
procedure TRST.SetH(valeur:boolean);
begin
h := valeur;
end;
function TRST.GetH : boolean;
begin
GetH := h;
end;
constructor TRST.Create;
begin
inherited;
setH(true);
end;
procedure TRST.SetS(valeur:boolean);
begin
inherited SetS(valeur AND GetH);
end;
procedure TRST.SetR(valeur:boolean);
begin
inherited SetR(valeur AND GetH);
end;
procedure TRST.afficher;
begin
inherited afficher;
writeln('H:',GetH);
end;
{*************** Bascule JK : CLASSES TJK hérite de TRST ***************}
Type TJK = class(TRST)
public
procedure SetJ(valeur:boolean);
procedure SetK(valeur:boolean);
end;
procedure TJK.SetJ(valeur:boolean);
begin
SetS(valeur AND GetQB);
end;
procedure TJK.SetK(valeur:boolean);
begin
SetR(valeur AND GetQ)
end;
var JK : TJK;
valeur : integer;
choix : char;
begin
JK := TJK.Create;
repeat
JK.afficher;
write ('(J)-(K)-(H)-(A)rret:');readln(choix);
Case choix of
'J' : begin
write ('J:');readln(valeur);JK.SetJ(valeur=1);
end;
'K' : begin
write ('K:');readln(valeur);JK.SetK(valeur=1);
end;
'H' : begin
write ('H:');readln(valeur);JK.SetH(valeur=1);
end;
end;
until choix='A';
JK.Destroy;
end.